практическое задание

 

Оценка результатов при малом числе измерений

 

Задание 1

    Ознакомьтесь с работой виртуального прибора Averaged.vi, отображающего взаимосвязь случайной погрешности измерений D, s (Error, на диаграмме показана красным цветом, распределение отображается на гистограмме D Histogram) со средним арифметическим этой же погрешности (Average Error, на диаграмме показана синим цветом, распределение отображается на гистограмме Average D Histogram) в зависимости от числа усредняемых n (Average from n=...). Заполните таблицу:

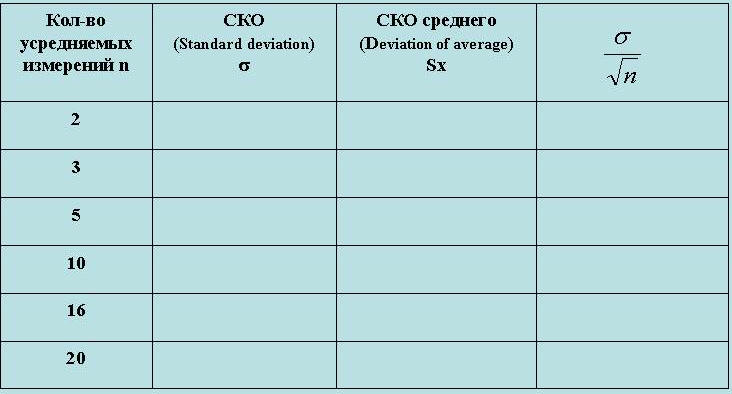
 Значения СКО среднего Sx определять при количестве измерений ("Number of points") N>10 000.

Сделайте вывод о связи СКО случайной погрешности измерений s с СКО среднего арифметического этой же погрешности Sx.

 

Задание 2

Ознакомьтесь с работой виртуального прибора Averaged uniform copy.vi. Прибор является точной копией прибора, приведенного в задании 1, но отображаемая погрешность измерения D распределена по иному (какому?) закону.

а) Проверьте, соблюдается ли для всех указанных в таблице n (при N>10 000) взаимосвязь СКО случайной погрешности измерений s с СКО среднего арифметического этой же погрешности Sx.

б) Определите для n=2 (при N>50 000) по какому закону распределена погрешность D и по какому закону распределено среднее арифметическое этой погрешности Average D. Сделайте эскиз обеих гистограмм, укажите на них наблюдаемые пределы погрешности, СКО, математическое ожидание погрешности.

в) Исходя из значения СКО случайной погрешности измерений s = 1, определите теоретически :

границы распределения погрешности измерения:

± D = ...;

значение СКО среднего арифметического для n=2:

Sx = ...;

границы распределения среднего арифметического для n=2:

± E = ... .

Сравните полученные значения с результатами наблюдений (пункт б)).

 

Задание 3

 

Взвешивание шести упаковок  с лекарством дало результаты, приведенные в таблице (варианты в столбцах) для Вашего варианта.

Определить границы доверительной погрешности ±E среднего для заданной в Вашем варианте доверительной вероятности, применив для расчета распределение Стьюдента. Результат вычислений округлить по правилам округления и представления результатов измерений  и записать согласно правилам выражений результатов измерений с предельными отклонениями, приведенным в п.8.5 ГОСТ 8.417-2002 "Единицы величин".

При симметричной доверительной погрешности результаты измерений представляют в форме

 

            X = ± Δ, P  

                       

где  - среднее арифметическое результатов измерений;

Δ – доверительная погрешность среднего;

Р - установленная вероятность, с которой погрешность измерения находится в этих границах.

 

Контрольные вопросы:

1. Является ли среднее арифметическое результатов серии измерений случайной величиной? Почему?

2. Может ли среднее арифметическое значение результатов серии измерений быть охарактеризовано дисперсией? Каким образом?

3. Как связаны дисперсия отдельных результатов измерений D(xi) и дисперсия среднего значения D() для равноточных  измерений?

4. Как определить оценку S среднего квадратического отклонения результата серии измерений  от xист?

5.  Каковы размерности следующих величин: математического ожидания М; доверительного интервала E; дисперсии D; коэффициента Стьюдента ts?

6. Каковы условия применения нормального закона для определения значения среднего квадра­тического отклонения S результата серии измерений?

7. В каком случае для определения значения среднего квадра­тического отклонения результата серии измерений применяют распределение Стьюдента?

8. От чего зависит плотность вероятности случайной погрешности измерений в распределении, предложенном Стьюдентом?

9. Как для распределения Стьюдента связаны доверительный интервал E и среднее квадра­тическое отклонение S результата серии измерений?

10. Какие законы распределения вероятности случайной погрешности измерений Вы знаете? Для какого из них предназначен математический аппарат распределения Стьюдента?  

 

 

Литература:

 

1. Сергеев А.Г., Крохин В.В. Метрология. М.: Логос. 2002 г.

2. Кузнецов В.А., Ялунина Г.В. Основы метрологии. Учебное пособие. - М.: ИПК Изд-во стандартов, 2001.

3. ГОСТ Р ИСО 5725-2002 Точность (правильность и прецизионность) методов и результатов измерений. М.: ИПК Изд-во стандартов, 2005. Часть 1. Основные положения и определения.

4. Рекомендации по межгосударственной стандартизации РМГ 29-99. Государственная система обеспечения единства измерений (ГСИ). «МЕТРОЛОГИЯ. Основные термины и определения» с Изменением № 1 от  2005 г. М.: ИПК Изд-во стандартов, 2005.

 

оглавление

практическая часть