оценка результатов при малом числе измерений

Как известно, для определения оценки S (или, в терминах теории вероятностей, ) рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, используют формулу Бесселя:

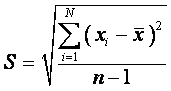, (1)

где x_i - результат i-го единичного измерения;

- среднее арифметическое значение измеряемой величины из n единичных результатов;

S (или ) - оценка рассеяния единичных результатов измерений - СКО.

Примечание - На практике широко распространен термин среднее квадратическое отклонение - (СКО). Под отклонением в соответствии с формулой (1) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин "погрешность измерения", целесообразно применять термин "средняя квадратическая погрешность".

После проведения серии измерений конкретной физической величины должно быть получено число, определяющее ее значение, и указана степень его достоверности, т. е. должен быть получен результат измерения. Но в данной серии из n измерений среднее арифметическое является линейной функцией результатов отдельных измерений x₁; x₂; x₃;… x_n, и, если произвести новую серию из п измерений, то вследствие влияния отдельных факторов значения x_i будут отличаться от полученных в первой серии, а следовательно, и новое значение будет иным.

Следовательно, , полученное в одной из серий измерений, является случайным приближением к x_ист. Чтобы иметь представление о возможных отклонениях от x_ист необходимо определить его среднее квадратическое отклонение. Вспомним свойства дисперсии независимых случайных величин из курса теории вероятностей:

Для конечного числа п независимых случайных величин:

D(x₁±x₂± x₃...± x_n)=D(x₁)+D(x₂)+...+D(x_n). (2)

Если x₁; x₂; x₃;… x_n – одинаково распределенные независимые случайные величины, дисперсия каждой из которых равна σ², то дисперсия их суммы равна п•σ², а дисперсия среднего арифметического равна σ²/п.

Так как результаты x_i отдельных измерений представляют взаимонезависимые случайные величины, то применяя теорему о дисперсии D линейной функции таких величин, можно записать

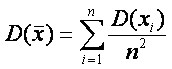(3)

Равноточность ряда измерений предполагает равенство всех отдельных D(x_i)= s², следовательно,

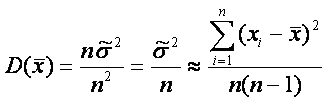(4).

Значит, средняя квадратическая погрешность результата измерений среднего арифметического (т.е. оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений) вычисляется по формуле:

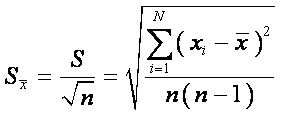(5)

где S - средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений;

n - число единичных измерений в ряду

Как мы помним из лабораторной работы №2, доверительные границы погрешности результата измерений , т.е. наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений, в случае нормального закона распределения вычисляются как ±tS, где S - средняя квадратическая погрешность единичного результата измерений; t - коэффициент, зависящий от доверительной вероятности P и числа измерений n.

Примечание. При симметричных границах термин может применяться в единственном числе - доверительная граница. Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности

Доверительную погрешность для среднего арифметического E также выражают через относительную величину t_S в долях среднего квадратического отклонения, т. е.

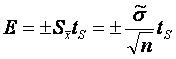(6).

Однако, если случайные величины x_i распределены по иному закону, чем нормальный, при небольшом числе измерений п вычисленное значение среднего квадратического отклонения среднего будет существенно отличаться от его действительного значения и в этом случае нормальный закон для определения доверительной погрешности среднего применять нельзя.

При малом числе повторных измерений п используют обычно распределение случайных погрешностей, предложенное У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Распределение (плотность вероятности) по этому закону зависит не только от значения случайной погрешности , но и от числа измерений n. Закон Стьюдента можно записать как

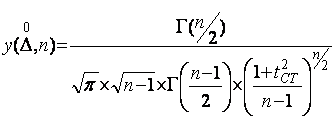(7)

где	у (, п)	- плотность вероятности случайной погрешности при заданном числе измерений п;
	Г(п)	- гамма-функция, значение которой зависит от числа измерений п и обладающая свойством Г(п+1)=п´ Г (п);
	tСТ	- параметр, определяемый выражением tСТ = /s, т. е. значение случайной погрешности, выраженное в долях среднего квадратического отклонения.

Графическое изображение кривых распределения (плотности вероятности) случайных погрешностей по закону Стьюдента, для различного числа измерений п показано на рис. 1.

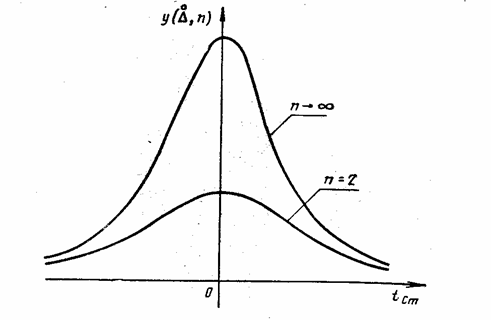
Рис. 1

На следующем рисунке показаны графики плотности распределения (дифференциальной функции распределения, привязан к левой оси ординат) и интегральной функции распределения (привязан к правой оси ординат) Стьюдента с тремя степенями свободы

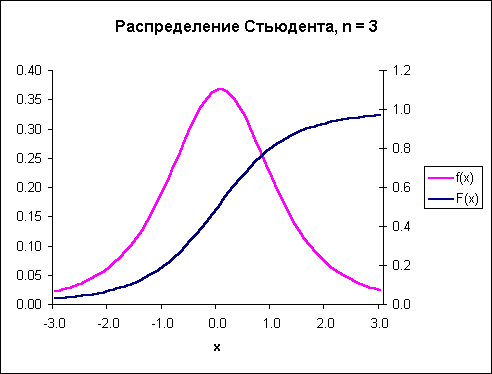
Рис. 2

Доверительная погрешность E и доверительная вероятность P_s(t) также зависят от числа измерений п (табл. 1 и 2).

Коэффициент Стьюдента t_s определяют по формуле

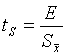(8).

где - среднее квадратическое отклонение среднего арифметического, определяемое по формуле (5).

При n®µ распределение Стьюдента совпадает с распределением по нормальному закону, а при n<20 оно резко отличается от нормального.

В начало главы

оглавление

практическая часть